 and
and
 ,
show that
,
show that
 if and only if
if and only if
 for each
for each
 .
.
Suppose that
 for each i. Let
for each i. Let
 . Choose
for each
. Choose
for each
 , a positive
, a positive
 such that for every
such that for every
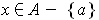 with
with
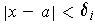 , one has
, one has
 .
Let
.
Let
 . Then, if
. Then, if
 satisfies
satisfies
 , then
, then
 .
So,
.
So,
 .
.
Conversely, suppose that
 ,
,
 , and
, and
 is chosen as in the definition of
is chosen as in the definition of
 . Then,
for each i, if
. Then,
for each i, if
 is in
is in
 and satisfies
and satisfies
 , then
, then
 . So
. So
 .
.
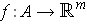 is continuous at
is continuous at
 if and
only if each
if and
only if each
 is.
is.
This is an immediate consequence of Problem 1-23 and the definition of continuity.
 is continuous.
is continuous.
By Problem 1-10, there is an
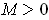 such that
such that
 for all
for all
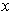 .
Let
.
Let
 and
and
 . Let
. Let
 .
If
.
If
 satisfies
satisfies
 , then
, then
 . So T is continuous at
. So T is continuous at
 .
.
 .
.
- Show that every straight line through
 contains an interval
around
contains an interval
around
 which is in
which is in
 .
.
Let the line be
 . If
. If
 , then the whole line is disjoint from
, then the whole line is disjoint from
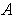 . On the other hand, if
. On the other hand, if
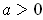 , then the line intersects the graph
of
, then the line intersects the graph
of
 at
at
 and
and
 and nowhere else.
Let
and nowhere else.
Let
 . Then
. Then
 is continuous
and
is continuous
and
 . Since the only roots of
. Since the only roots of
 are at 0 and
are at 0 and
 , it follows
by the intermediate value theorem that
, it follows
by the intermediate value theorem that
 for all
for all
 with
with
 .
In particular, the line
.
In particular, the line
 cannot intersect
cannot intersect
 anywhere to the left of
anywhere to the left of
 .
.
- Define
 by
by
 if
if
 and
and
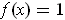 if
if
 . For
. For
 define
define
 by
by
 . Show that each
. Show that each
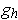 is continuous at 0, but
is continuous at 0, but
 is not
continuous at
is not
continuous at
 .
.
For each
 ,
,
 is identically zero in a neighborhood of zero by part (a).
So, every
is identically zero in a neighborhood of zero by part (a).
So, every
 is clearly continuous at 0. On the other hand,
is clearly continuous at 0. On the other hand,
 cannot
be continuous at
cannot
be continuous at
 because every open rectangle containing
because every open rectangle containing
 contains points of
contains points of
 and for all those points
and for all those points
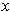 , one has
, one has
 .
.
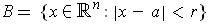 is open by
considering the function
is open by
considering the function
 with
with
 .
.
The function
 is continuous. In fact, let
is continuous. In fact, let
 and
and
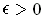 .
Let
.
Let
 . If
. If
 , then
by Problem 1-4, one has:
, then
by Problem 1-4, one has:
 .
This proves that
.
This proves that
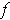 is continuous.
is continuous.
Since
 , it follows that
, it follows that
 is open by Theorem 1-8.
is open by Theorem 1-8.
 is not closed, show that there is a
continuous function
is not closed, show that there is a
continuous function
 which is unbounded.
which is unbounded.
As suggested, choose
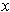 to be a boundary point of
to be a boundary point of
 which is not in
which is not in
 ,
and let
,
and let
 . Clearly, this is unbounded. To show it is
continuous at
. Clearly, this is unbounded. To show it is
continuous at
 , let
, let
 and choose
and choose
 .
Then for any
.
Then for any
 with
with
 , one has
, one has
 .
So,
.
So,

where we have used Problem 1-4 in
the simplification. This shows that
 is continuous at
is continuous at
 .
.
 is compact, prove that every continuous function
is compact, prove that every continuous function
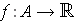 takes on a maximum and a minimum value.
takes on a maximum and a minimum value.
By Theorem 1-9,
 is compact, and hence is closed and bounded. Let
is compact, and hence is closed and bounded. Let
 (resp.
(resp.
 ) be the greatest lower bound (respectively least upper
bound) of
) be the greatest lower bound (respectively least upper
bound) of
 . Then
. Then
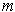 and
and
 are boundary points of
are boundary points of
 , and hence
are in
, and hence
are in
 since it is closed. Clearly these are the minimum and
maximum values of
since it is closed. Clearly these are the minimum and
maximum values of
 , and they are taken on since they are in
, and they are taken on since they are in
 .
.
 be an increasing function.
If
be an increasing function.
If
 are distinct, show that
are distinct, show that
 .
.
One has
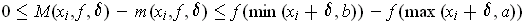 . The function on the right is an increasing
function of
. The function on the right is an increasing
function of
 ; in particular,
; in particular,
 is bounded above by the
quantity on the right for any
is bounded above by the
quantity on the right for any
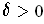 . Now assume that the
. Now assume that the
 have
been re-ordered so that they are in increasing order; let
have
been re-ordered so that they are in increasing order; let
 . Now add up all the inequalities
with this value of
. Now add up all the inequalities
with this value of
 ; it is an upper bound for the sum of the
; it is an upper bound for the sum of the
 and the right hand side ``telescopes" and is bounded above by the
difference of the two end terms which in turn is bounded above by
and the right hand side ``telescopes" and is bounded above by the
difference of the two end terms which in turn is bounded above by
 .
.