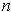 -manifold with boundary in
-manifold with boundary in
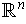 .
.
The generalization: Let
 be a compact
be a compact
 -dimensional
manifold-with-boundary and
-dimensional
manifold-with-boundary and
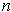 the unit outward normal on
the unit outward normal on
 .
Let
.
Let
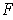 be a differentiable vector fieldd on
be a differentiable vector fieldd on
 . Then
. Then

As in the proof of the divergence theorem, let
 . Then
. Then
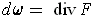 . By Problem 5-25,
on
. By Problem 5-25,
on
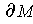 , we have
, we have
 for
for
 . So,
. So,

By Stokes' Theorem, it follows that

 and
and
 , find the volume of
, find the volume of
 in terms of the
in terms of the
 -dimensional volume
of
-dimensional volume
of
 . (This volume is
. (This volume is
 if
if
 is even and
is even and
 if
if
 is odd.)
is odd.)
One has
 and
and
 since the outward
normal is in the radial direction. So
since the outward
normal is in the radial direction. So
 . In particular, if
. In particular, if
 , this says
the surface area of
, this says
the surface area of
 is
is
 times the volume of
times the volume of
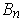 .
.
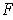 on
on
 by
by
 and let
and let
 be a compact three-dimensional manifold-with-boundary with
be a compact three-dimensional manifold-with-boundary with
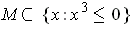 . The vector field
. The vector field
 may be thought of as the downward
pressure of a fluid of density
may be thought of as the downward
pressure of a fluid of density
 in
in
 . Since a fluid
exerts equal pressures in all directions, we define the buoyaant
force on
. Since a fluid
exerts equal pressures in all directions, we define the buoyaant
force on
 , due to the fluid, as
, due to the fluid, as
 . Prove
the following theorem.
. Prove
the following theorem.
Theorem (Archimedes). The buoyant force on
 is equal to the weight of the
fluid displaced by
is equal to the weight of the
fluid displaced by
 .
.
The definition of buoyant force is off by a sign.
The divergence theorem gives
 . Now
. Now
 is the weight of the fluid displaced
by
is the weight of the fluid displaced
by
 . So the right hand side should be the buoyant force. So one has
the result if we define the buoyant force to be
. So the right hand side should be the buoyant force. So one has
the result if we define the buoyant force to be
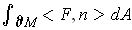 .
(This would make sense otherwise the buoyant force would be negative.)
.
(This would make sense otherwise the buoyant force would be negative.)