Exercises: Chapter 5, Section 4

  1. If ch5d1.png is an oriented one-dimensional manifold in ch5d2.png and ch5d3.png is orientation-preserving, show that

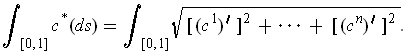
    ch5d4.png

    Consider the 1-form defined by ch5d5.png . This is the form which matches the proposed solution since

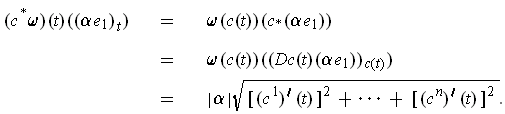
    ch5d6.png

    Furthermore, it is the volume element. To see this, choose an orthonormal basis ch5d7.png where ch5d8.png where ch5d9.png . Then ch5d10.png and ch5d11.png if and only if ch5d12.png , as desired.

  2. If ch5d13.png is an ch5d14.png -dimensional manifold in ch5d15.png , with the usual orientation, show that ch5d16.png , so that the volume of ch5d17.png , as defined in this section, is the volume as defined in Chapter 3. (Note that this depends on the numerical factor in the definition of ch5d18.png .)

    Let ch5d19.png be an orientation-preserving ch5d20.png -cube, i.e. ch5d21.png . Let ch5d22.png be an orthonormal basis with the usual orientation. By Theorem 4-9, we have ch5d23.png and so applying this to ch5d24.png gives

    ch5d25.png

    Since ch5d26.png is orientation preserving, it must be that ch5d27.png .

    Now,

    ch5d28.png

    Now, ch5d29.png is orientation preserving, so ch5d30.png must have the usual orientation, i.e. ch5d31.png . But then ch5d32.png . Since this is also equal to ch5d33.png by orthonormality, it follows that the value is precisely 1, and so it is the volume element in the sense of this section.

  3. Generalize Theorem 5-6 to the case of an oriented ch5d34.png -dimensional manifold in ch5d35.png .

    The generalization is ch5d36.png defined by

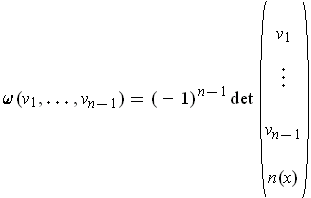
    ch5d37.png

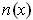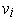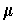    where ch5d38.png is the unit outward normal at ch5d39.png . As in the 2-dimensional case, ch5d40.png if the ch5d41.png are an orthonormal basis with orientation ch5d42.png (where ch5d43.png was the orientation used to determine the outward normal). So ch5d44.png is the volume element ch5d45.png .

    Expanding in terms of cofactors of the last row gives:

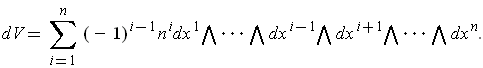
    ch5d46.png

    As in the 2-dimensional case, ch5d47.png for some scalar ch5d48.png and so

    ch5d49.png

    for all ch5d50.png . Letting ch5d51.png , we get

    ch5d52.png

    1. If ch5d53.png is non-negative and the graph of ch5d54.png in the ch5d55.png -plane is revolved around the ch5d56.png -axis in ch5d57.png to yield a surface ch5d58.png , show that the area of ch5d59.png is

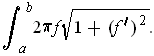
      ch5d60.png

      One can use singular 2-cubes of the form ch5d61.png . The quantities ch5d62.png , ch5d63.png , and ch5d64.png calculate out to ch5d65.png , ch5d66.png , and ch5d67.png . So the surface area is ch5d68.png .

    2. Compute the area of ch5d69.png .

      Apply part (a) with ch5d70.png and ch5d71.png . One has ch5d72.png and ch5d73.png . So ch5d74.png .

  5. If ch5d75.png is a norm preserving linear transformation and ch5d76.png is a ch5d77.png -dimensional manifold in ch5d78.png , show that ch5d79.png has the same volume as ch5d80.png .

    Although it is not stated, it is assumed that ch5d81.png is orientable.

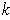    By Problem 1-7, ch5d82.png is inner product preserving and so it maps orthonormal bases to orthonormal bases. Further, if ch5d83.png is a singular ch5d84.png -cube which is a coordinate system for ch5d85.png in a neighborhood of ch5d86.png , then ch5d87.png is a singular ch5d88.png -cube which is a coordinate system for ch5d89.png in a neighborhood of ch5d90.png . Depending on the sign of ch5d91.png , the new ch5d92.png -cube is either orientation preserving or reversing. 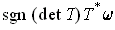In particular, ch5d93.png is the volume element of ch5d94.png if ch5d95.png is the volume element of ch5d96.png (which is also orientable). Since the volume is just the integral of the volume element and the integral is calculated via the ch5d97.png -cubes, it follows that the volumes of ch5d98.png and ch5d99.png are equal.

    1. If ch5d100.png is a ch5d101.png -dimensional manifold, show that an absolute ch5d102.png -tensor |dV| can be defined, even if ch5d103.png is not orientable, so that the volume of 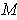ch5d104.png can be defined as ch5d105.png .

      This was already done in Problem 5-21.

    2. If ch5d106.png is defined by

      ch5d107.png

      show that ch5d108.png is a M@ouml;bius strip and find its area.

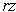      To see that it is a M@ouml;bius strip, note that in cylindrical coordinates, the equations are: ch5d109.png . In particular, for fixed ch5d110.png , we have ch5d111.png fixed and the path is a line segment traversed from ch5d112.png to ch5d113.png . Calculating the length of the line, one gets that is a line segment of length 2. Again, for fixed ch5d114.png , the line segment in the ch5d115.png -plane has slope ch5d116.png . 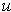Note that this varies from ch5d117.png down to ch5d118.png as ch5d119.png ranges from 0 to ch5d120.png , i.e. 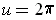the line segment starts vertically at ch5d121.png and reduces in slope until it becomes vertical again at ch5d122.png . This corresponds to twisting the paper 180 degrees as it goes around the ring, which is the M@ouml;bius strip.

      To find the area, one can actually, just use the formulas for an orientable surface, since one can just remove the line at ch5d123.png . In thatt case one can verify, preferably with machine help, that ch5d124.png , ch5d125.png , and ch5d126.png . So the area is ch5d127.png . Numerical evaluation of the integral yields the approximation ch5d128.png , which is just slightly larger than ch5d129.png , the area of a circular ring of radius 2 and height 2.

  7. If there is a nowhere-zero ch5d130.png -form on a ch5d131.png -dimensional manifold ch5d132.png , show that ch5d133.png is orientable

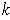    Suppose ch5d134.png is the nowhere-zero ch5d135.png -form on ch5d136.png . If ch5d137.png is a singular ch5d138.png -cube, then for every ch5d139.png , we have ch5d140.png because the space ch5d141.png is of dimension 1. Choose a ch5d142.png -cube so that the value is positive for some p. Then if it were negative at another point ch5d143.png , then because this is a continuous function from ch5d144.png into ch5d145.png , the intermediate value theorem would guarantee a point ch5d146.png where the function were zero, which is absurd. 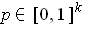So the value is positive for all ch5d147.png .

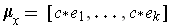    For every ch5d148.png , choose a ch5d149.png -cube of this type with ch5d150.png in its image. Define ch5d151.png . This is well defined. Indeed, if we had two such ch5d152.png -cubes, say ch5d153.png and ch5d154.png , then the ch5d155.png (where ch5d156.png ) are positive for ch5d157.png . But then the values are of the same sign regardless of which non-zero k-form in ch5d158.png is used. So, both maps define the same orientation on ch5d159.png .

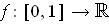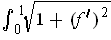    1. If ch5d160.png is differentiable and ch5d161.png is defined by ch5d162.png , show that ch5d163.png has length ch5d164.png .

      This is an immediate consequence of Problem 5-23.

    2. Show that this length is the least upper bound of lengths of inscribed broken lines.

      We will need ch5d165.png to be continuously differentiable, not just differentiable.

      Following the hint, if ch5d166.png , then by the mean value theorem,

      ch5d167.png

      for some ch5d168.png . Summing over ch5d169.png gives a Riemann sum for ch5d170.png . Taking the limit as the mesh approaches 0, shows that these approach the integral. Starting from any partition, and taking successively finer partitions of the interval with the mesh approaching zero, we get an increasing sequence of values with limit the value of the integral; so the integral is the least upper bound of all these lengths.

  9. Consider the 2-form ch5d171.png defined on ch5d172.png by

    ch5d173.png

    1. Show that ch5d174.png is closed.

      This is a straightforward calculation using the definition and Theorem 4-10. For example, 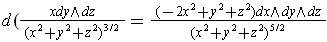ch5d175.png . The other two terms give similar results, and the sum is zero.

    2. Show that

      ch5d176.png

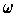      For ch5d177.png let ch5d178.png . Show that ch5d179.png restricted to the tangent space of ch5d180.png is ch5d181.png times the volume element and that ch5d182.png . Conclude that ch5d183.png is not exact. Nevertheless, we denote ch5d184.png by ch5d185.png since, as we shall see, ch5d186.png is the analogue of the 1-form ch5d187.png on ch5d188.png .

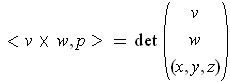      As in the proof of Theorem 5-6 (or Problem 5-25), the value of ch5d189.png can be evaluated by expanding ch5d190.png using cofactors of the third row.

      The second assertion follows from ch5d191.png and the fact that the outward directed normal can be taken to be ch5d192.png be an appropriate choice of orientation. One has ch5d193.png by Problem 5-26.

      If ch5d194.png , then Stokes' Theorem would imply that ch5d195.png . Since the value is ch5d196.png , we conclude that ch5d197.png is not exact.

    3. If ch5d198.png is a tangent vector such that ch5d199.png for some ch5d200.png , show that ch5d201.png for all ch5d202.png . If a two-dimensional manifold ch5d203.png in ch5d204.png is part of a generalized cone, that is, ch5d205.png is the union of segments of rays through the origin, show that ch5d206.png .

      If ch5d207.png , then using part (b), one has ch5d208.png . By Problem 5-9, for any point ch5d209.png on the generalized cone, the line through ch5d210.png and the origin lies on the surface and so its tangent line (the same line) is in ch5d211.png . But then ch5d212.png is identically 0 for all points ch5d213.png . But then ch5d214.png .

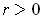    4. Let ch5d215.png be a compact two-dimensionaal manifold-with-boundary such that every ray through 0 intersects ch5d216.png at most once (Figure 5-10). The union of those rays through 0 which intersect ch5d217.png , is a solid cone ch5d218.png . The solid angle subtended by ch5d219.png is defined as the area of ch5d220.png , or equivalently as ch5d221.png times the area of ch5d222.png for ch5d223.png . Prove that the solid angle subtended by ch5d224.png is ch5d225.png .

      We take the orientations induced from the usual orientation of ch5d226.png .

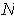      Following the hint, choose ch5d227.png small enough so that there is a three dimensional manifold-with-boundary N (as in Figure 5-10) such that ch5d228.png is the union of ch5d229.png and ch5d230.png , and a part of a generalized cone. (Actually, ch5d231.png will be a manifold-with-corners; see the remarks at the end of the next section.)

      Note that this is essentially the same situation as in Problem 5-22. Applying Stokes' Theorem gives ch5d232.png because ch5d233.png is closed by part (a). By part (c), the integral over the part of the boundary making up part of a generalized cone is zero. The orientation of the part of the boundary on ch5d234.png is opposite to that of the orientation of the same set as a part of ch5d235.png . So, we have ch5d236.png and the last integral is the solid angle subtended by ch5d237.png by the interpretation of ch5d238.png of part (b).

  10. Let ch5d239.png be nonintersecting closed curves. Define the linking number l(f,g) of ch5d240.png and ch5d241.png by (cf. Problem 4-34

    ch5d242.png

    }

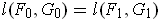    1. Show that if (F,G) is a homotopy of nonintersecting closed curves, then ch5d243.png .

      This follows immediately from Problem 4-34 (b) and Problem 5-31 (a).

    2. If ch5d244.png show that

      ch5d245.png

      where

      ch5d246.png

      This follows by direct substitution using the expression for ch5d247.png in the preamble to Problem 31.

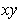    3. Show that ch5d248.png if ch5d249.png and ch5d250.png both lie in the ch5d251.png -plane.

      This follows from the formula in part (b) since the third column of the determinant defining ch5d252.png is zero.

    The curves of Figure 4-5(b) are given by 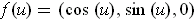ch5d253.png and ch5d254.png . You may easily convince yourself that calculating ch5d255.png by the above integral is hopeless in this case. The following problem shows how to find ch5d256.png without explicit calculations.

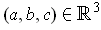    1. If ch5d257.png define

      ch5d258.png

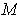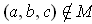      If ch5d259.png is a compact two-dimensional manifold-with-boundary in ch5d260.png and ch5d261.png define

      ch5d262.png

      Let ch5d263.png be a point on the same side of ch5d264.png as the outward normal and ch5d265.png be a point on the opposite side. Show that by choosing ch5d266.png sufficiently close to ch5d267.png we can make ch5d268.png as close to ch5d269.png as desired.

      Following the hint, suppose that ch5d270.png where ch5d271.png is a compact manifold-with-boundary of dimension 3. Suppose ch5d272.png . Removing a ball centered at ch5d273.png from the interior of ch5d274.png gives another manifold-with-boundary ch5d275.png with boundary ch5d276.png , where the orientation on ch5d277.png is opposite to that of the induced orientation. So by Stokes' Theorem and Problem 5-31 (b), ch5d278.png . 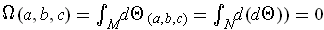(Note the discrepancy in sign between this and the hint.) On the other hand, if ch5d279.png , then by Stokes' Theorem, ch5d280.png .

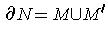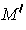      The rest of the proof will be valid only in the case where there is a 3-dimensional compact oriented manifold-with-boundary ch5d281.png such that ch5d282.png where ch5d283.png is a two-dimensional manifold. Then ch5d284.png , and and we can take ch5d285.png . So, ch5d286.png and ch5d287.png by the last paragraph. Subtracting gives ch5d288.png . The first term can be made as small as we like by making ch5d289.png sufficiently small.

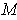    2. Suppose ch5d290.png for some compact oriented two-dimensional manifold-with-boundary ch5d291.png . (If ch5d292.png does not intersect itself such an ch5d293.png always exists, even if ch5d294.png is knotted, see [6], page 138.) Suppose that whenever ch5d295.png intersects ch5d296.png at ch5d297.png , the tangent vector ch5d298.png of ch5d299.png is not in ch5d300.png . Let ch5d301.png be the number of intersections where ch5d302.png points in the same direction as the outward normal, and ch5d303.png the number of other intersections. If ch5d304.png , show that

      ch5d305.png

      In the statement, what one means is that the component of ch5d306.png in the outward normal direction is either in the same or opposite direction as the outward normal.

      Parameterize ch5d307.png with ch5d308.png where ch5d309.png is not in ch5d310.png . Let ch5d311.png be the values where ch5d312.png intersects ch5d313.png . To complete the proof, we will need to assume that ch5d314.png is finite. Let 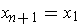ch5d315.png . Choose ch5d316.png small enough so that ch5d317.png for all ch5d318.png (where by ch5d319.png we mean ch5d320.png . One has

      ch5d321.png

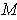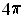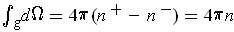      By part (a), if the tangent vector to ch5d322.png at ch5d323.png has a component in the outward normal direction of ch5d324.png is positive, then ch5d325.png is ch5d326.png ; if it is negative, then it is ch5d327.png . So, the last paragraph has ch5d328.png .

      Note that this result differs from the problem statement by a sign.

    3. Prove that

      ch5d329.png

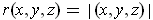      where ch5d330.png .

      The definition of ch5d331.png should be ch5d332.png .

      The proofs are analogous; we will show the first result. Start with

      ch5d333.png

      where we have used Problem 3-32 to interchange the order of the limit and the integral.

      On the other hand, we have by Stokes' Theorem that

      ch5d334.png

      Comparing the two expressions, we see that two of the terms in the first expression match up with corresponding terms in the second expression. It remains to check that the remaining terms are equal. But a straightforward expansion gives: ch5d335.png as desired.

    4. Show that the integer ch5d336.png of (b) equals the integral of Problem 5-32(b), and use this result to show that ch5d337.png if ch5d338.png and ch5d339.png are the curves of Figure 4-6 (b), while ch5d340.png if ch5d341.png and ch5d342.png are the curves of Figure 4-6 (c). (These results were known to Gauss [7]. The proofs outlined here are from [4] pp. 409-411; see also [13], Volume 2, pp. 41-43.)

      By part (c), one has ch5d343.png and so ch5d344.png . Similar results hold for ch5d345.png and ch5d346.png . One then substitutes into: ch5d347.png . After collecting terms, we see that this is equal to the expression for ch5d348.png in Problem 5-32 (b). So, ch5d349.png .

      By inspection in Figure 4-6, one has ch5d350.png and ch5d351.png in parts (b) and (c) of the figure. So, these are also the values of ch5d352.png .