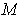 is an
is an
 -dimensional manifold (or manifold-with-boundary)
in
-dimensional manifold (or manifold-with-boundary)
in
 , with the usual orientation, show that
, with the usual orientation, show that
 ,
as defined in this section, is the same as
,
as defined in this section, is the same as
 , as defined in Chapter 3.
, as defined in Chapter 3.
We can assume in the situation of Chapter 3 that
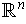 has the usual
orientation. The singular
has the usual
orientation. The singular
 -cubes with
-cubes with
 can be taken
to be linear maps
can be taken
to be linear maps
 where
where
 and
and
 are scalar constants.
One has with
are scalar constants.
One has with
 , that
, that
 . So, the two integrals give the
same value.
. So, the two integrals give the
same value.
- Show that Theorem 5-5 is false if
 is not required to be compact.
is not required to be compact.
For example, if we let
 be the open interval
be the open interval
 , one has
, one has
 but
but
 . One can also let
. One can also let
 and
and
 .
.
- Show that Theorem 5-5 holds for noncompact
 provided that
provided that
 vanishes outside of a compact subset of
vanishes outside of a compact subset of
 .
.
The compactness was used to guarantee that the sums in the proof were finite; it also works under this assumption because all but finitely many summands are zero if
 vanishes outside of a compact subset of
vanishes outside of a compact subset of
 .
.
 is a
is a
 -form on a compact
-form on a compact
 -dimensional
manifold
-dimensional
manifold
 , prove that
, prove that
 . Give a counter-example
if
. Give a counter-example
if
 is not compact.
is not compact.
One has
 as
as
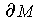 is
empty. With
is
empty. With
 the set of positive real numbers, one has with
the set of positive real numbers, one has with
 that
that
 .
.
 -tensor on
-tensor on
 is a function
is a function
 of the form
of the form
 for
for
 .
An absolute
.
An absolute
 -form on
-form on
 is a function
is a function
 such that
such that
 is an absolute
is an absolute
 -tensor on
-tensor on
 . Show that
. Show that
 can be
defined, even if
can be
defined, even if
 is not orientable.
is not orientable.
Make the definition the same as done in the section, except don't require
the manifold be orientable, nor that the singular
 -cubes be orientation
preserving. In order for this to work, we need to have the argument of
Theorem 5-4 work, and there the crucial step was to replace
-cubes be orientation
preserving. In order for this to work, we need to have the argument of
Theorem 5-4 work, and there the crucial step was to replace
 with its absolute value so that Theorem 3-13 could be applied. In our case,
this is automatic because Theorem 4-9 gives
with its absolute value so that Theorem 3-13 could be applied. In our case,
this is automatic because Theorem 4-9 gives
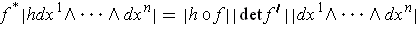 .
.
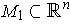 is an
is an
 -dimensional manifold-with-boundary
and
-dimensional manifold-with-boundary
and
 is an
is an
 -dimensional manifold with
boundary, and
-dimensional manifold with
boundary, and
 are compact, prove that
are compact, prove that

where
 is an
is an
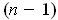 -form on
-form on
 , and
, and
 and
and
 have the orientations induced by the usual orieentations of
have the orientations induced by the usual orieentations of
 and
and
 .
.
Following the hint, let
 . Then
. Then
 is an
is an
 -dimensional manifold-with-boundary and its boundary is the union of
-dimensional manifold-with-boundary and its boundary is the union of
 and
and
 . Because the outward directed normals
at points of
. Because the outward directed normals
at points of
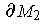 are in opposite directions for
are in opposite directions for
 and
and
 ,
the orientation of
,
the orientation of
 are opposite in the two cases. By Stokes'
Theorem, we have
are opposite in the two cases. By Stokes'
Theorem, we have
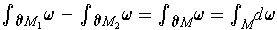 . So the result is equivalent
to
. So the result is equivalent
to
 . So, the result, as stated, is not correct; but,
for example, it would be true if
. So, the result, as stated, is not correct; but,
for example, it would be true if
 were closed.
were closed.