Exercises: Chapter 5, Section 1

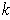  1. If ch5a1.png is a ch5a2.png -dimensional manifold with boundary, prove that ch5a3.png is a ch5a4.png -dimensional manifold and ch5a5.png is a ch5a6.png =dimensional manifold.

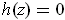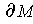    The boundary of ch5a7.png is the set of points ch5a8.png which satisfy condition ch5a9.png . Let ch5a10.png be as in condition ch5a11.png ; then the same ch5a12.png works for every point in ch5a13.png such that ch5a14.png . In particular, each such ch5a15.png is in ch5a16.png . Further, ch5a17.png also is map which shows that condition ch5a18.png is satisfied for each such ch5a19.png . So ch5a20.png is a manifold of dimension ch5a21.png , and because those points which don't satisfy ch5a22.png must satisfy ch5a23.png , it follows that ch5a24.png is a manifold of dimension ch5a25.png .

  2. Find a counter-example to Theorem 5-2 if condition (3) is omitted.

    Following the hint, consider ch5a26.png defined by

    ch5a27.png

    Let ch5a28.png , ch5a29.png , ch5a30.png , ch5a31.png . Then condition ch5a32.png holds except for part (3) since ch5a33.png

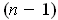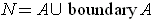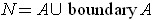    1. Let ch5a34.png be an open set such that boundary ch5a35.png is an ch5a36.png -dimensional manifold. Show that ch5a37.png is an ch5a38.png -dimensional manifold with boundary. (It is well to bear in mind the following example: if ch5a39.png , then ch5a40.png is a manifold with boundary, but ch5a41.png .)

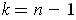      Since ch5a42.png is open, each of its points satisfies condition ch5a43.png with ch5a44.png . Let ch5a45.png . Then ch5a46.png satisfies ch5a47.png with ch5a48.png , say with the function ch5a49.png . Let ch5a50.png be one of the half-planes ch5a51.png or ch5a52.png Suppose there is a sequence ch5a53.png of points of ch5a54.png such that the ch5a55.png all lie in ch5a56.png and converge to ch5a57.png . If there is no open neighborhood ch5a58.png of ch5a59.png such that ch5a60.png , then there is a sequence ch5a61.png of points of ch5a62.png such that the sequence converges to ch5a63.png . But then the line segments from ch5a64.png to ch5a65.png must contain a point o the boundary of ch5a66.png , which is absurd since the points of U in the boundary of ch5a67.png all map to points with last coordinate 0. 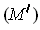It follows that h restricted to an appropriately small open subset of ch5a68.png either satisfies condition ch5a69.png or condition ch5a70.png . This proves the assertion.

    2. Prove a similar assertion for an open subset of an n-dimensional manifold.

      The generalization to manifolds is proved in the same way, except you need to restrict attention to a coordinate system around ch5a71.png . By working in the set ch5a72.png of condition ch5a73.png , one gets back into the case where one is contained within ch5a74.png , and the same argument applies.

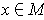  4. Prove a partial converse to Theorem 5-1: If ch5a75.png is a ch5a76.png -dimensional manifold and ch5a77.png , then there is an open set ch5a78.png containing ch5a79.png and a differentiable function ch5a80.png such that ch5a81.png and ch5a82.png has rank ch5a83.png when ch5a84.png .

    Let ch5a85.png be as in condition ch5a86.png applied to ch5a87.png , ch5a88.png , and ch5a89.png be defined by ch5a90.png . Then the function ch5a91.png satisfies all the desired conditions.

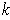  5. Prove that a ch5a92.png -dimensional (vector) subspace of ch5a93.png is a ch5a94.png -dimensional manifold.

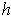    Let ch5a95.png be a basis for the subspace, and choose ch5a96.png so that all the ch5a97.png together form a basis for ch5a98.png . Define a map ch5a99.png by ch5a100.png . One can verify that ch5a101.png satisfies the condition ch5a102.png .

  6. If ch5a103.png , the graph of ch5a104.png is ch5a105.png . Show that the graph of ch5a106.png is an ch5a107.png -dimensional manifold if and only if ch5a108.png is differentiable.

    If ch5a109.png is differentiable, the map ch5a110.png defined by ch5a111.png is easily verified to be a coordinate system around all points of the graph of f; so the graph is a manifold of dimension n.

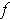    Conversely, suppose ch5a112.png is as in condition ch5a113.png for some point ch5a114.png in the graph. Let ch5a115.png be the projection on the last ch5a116.png coordinates. Then apply the Implicit function theorem to ch5a117.png . The differentiable function ch5a118.png obtained from this theorem must be none other than ch5a119.png since the graph is the set of points which map to zero by ch5a120.png .

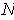  7. Let ch5a121.png . If ch5a122.png is a ch5a123.png -dimensional manifold and ch5a124.png is obtained by revolving ch5a125.png around the axis ch5a126.png , show that ch5a127.png is a ch5a128.png -dimensional manifold. Example: the torus (Figure 5-4).

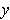    Consider the case where n = 3. If ch5a129.png is defined in some open set by ch5a130.png , then ch5a131.png is defined by ch5a132.png . The Jacobian is ch5a133.png Since either ch5a134.png or ch5a135.png is non-zero, it is easy to see that the Jacobian has the proper rank.

    In the case where n > 3, it is not obvious what one means by ``rotate".

    1. If ch5a136.png is a ch5a137.png -dimensional manifold in ch5a138.png and ch5a139.png , show that ch5a140.png has measure 0.

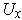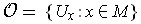      For each ch5a141.png , one has condition ch5a142.png holding for some function ch5a143.png . Let ch5a144.png be the domain of one of these functions, where we can choose ch5a145.png to be a ball with center at rational coordinates and rational radius. Then ch5a146.png is a countable cover of ch5a147.png . 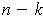Now each ch5a148.png maps points of ch5a149.png in ch5a150.png to points with the last ch5a151.png coordinates 0. Take a thin plate including the image of ch5a152.png ; its inverse image has volume which can be bounded by ch5a153.png where ch5a154.png is the volume of the plate (by the change of variables formula). By choosing the thickness of the plate sufficiently small, we can guarantee that this value is no more than ch5a155.png for the ch5a156.png element of the cover. This shows the result.

    2. If ch5a157.png is a closed ch5a158.png -dimensional manifold with boundary in ch5a159.png , show that the boundary of ch5a160.png is ch5a161.png . Give a counter-example if ch5a162.png is not closed.

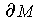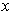      Clearly, every element of ch5a163.png is in the boundary of ch5a164.png by the condition ch5a165.png . If ch5a166.png is in the boundary of ch5a167.png , then ch5a168.png since ch5a169.png is closed. So if ch5a170.png , it must satisfy condition ch5a171.png . But then ch5a172.png is in the interior of ch5a173.png because the dimension of ch5a174.png is n.

      The open unit interval in ch5a175.png is a counter-example if we do not require ch5a176.png to be closed.

    3. If ch5a177.png is a compact ch5a178.png -dimensional manifold with boundary in ch5a179.png , show that ch5a180.png is Jordan-measurable.

      By part (b), the boundary of ch5a181.png is ch5a182.png . By Problem 5-1, ch5a183.png is an ch5a184.png -dimensional manifold contained in ch5a185.png . By part (a), it follows that ch5a186.png is of measure 0. Finally, since ch5a187.png is bounded, the definition of Jordan measurable is satisfied.