Let
 be a collection of open sets, and
be a collection of open sets, and
 be their union.
If
be their union.
If
 , then there is an
, then there is an
 with
with
 . Since
. Since
 is
open, there is an open rectangle
is
open, there is an open rectangle
 containing
containing
 .
So
.
So
 is open.
is open.
Let
 and
and
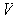 be open, and
be open, and
 . If
. If
 , then
there are open rectangles
, then
there are open rectangles
 (resp.
(resp.
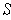 ) containing
) containing
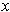 and contained in
and contained in
 (resp.
(resp.
 ). Since the intersection of two open rectangles is an open
rectangle (Why?), we have
). Since the intersection of two open rectangles is an open
rectangle (Why?), we have
 ; so
; so
 is open.
The assertion about finitely many sets follows by induction.
is open.
The assertion about finitely many sets follows by induction.
The intersection of the open intervals
 is the set containing only
is the set containing only
 , and so the intersection of even countably many open sets is not necessarily
open.
, and so the intersection of even countably many open sets is not necessarily
open.
 is open.
is open.
If
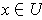 , then let
, then let
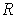 be the open rectangle centered at
be the open rectangle centered at
 with
sides of length
with
sides of length
 . If
. If
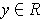 , then
, then

and so
 . This proves that
. This proves that
 is open.
is open.
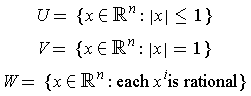
The interior of
 is the set
is the set
 ; the exterior is
; the exterior is
 ;
and the boundary is the set
;
and the boundary is the set
 .
.
The interior of
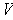 is the empty set
is the empty set
 ; the exterior is
; the exterior is
 ;
and the boundary is the set
;
and the boundary is the set
 .
.
The interior of
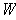 is the empty set
is the empty set
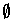 ; the exterior is the empty set
; the exterior is the empty set
 ;
and the boundary is the set
;
and the boundary is the set
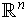 .
.
In each case, the proofs are straightforward and omitted.
 such that
such that
 contains at most one point on each horizontal and each vertical line but the
boundary of
contains at most one point on each horizontal and each vertical line but the
boundary of
 is
is
 . Hint: It suffices to ensure
that
. Hint: It suffices to ensure
that
 contains points in each quarter of the square
contains points in each quarter of the square
 and also in each sixteenth, etc.
and also in each sixteenth, etc.
To do the construction, first make a list
 of all the rational numbers
in the interval [0, 1]. Then make a list
of all the rational numbers
in the interval [0, 1]. Then make a list
 of all the quarters, sixteenths, etc.
of the unit sqare. For example,
of all the quarters, sixteenths, etc.
of the unit sqare. For example,
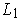 could be made by listing all pairs
(a, b) of integers with
could be made by listing all pairs
(a, b) of integers with
 positive,
positive,
 non-negative,
non-negative,
 , in increasing order
of
, in increasing order
of
 , and amongst those with same value of
, and amongst those with same value of
 in increasing
lexicographical order; then simply eliminate those pairs for which there is
an earlier pair with the same value of
in increasing
lexicographical order; then simply eliminate those pairs for which there is
an earlier pair with the same value of
 . Similarly, one could make
. Similarly, one could make
 by listing first the quarters, then the sixteenths, etc. with an obvious
lexicographical order amongst the quarters, sixteenths, etc. Now, traverse
the list
by listing first the quarters, then the sixteenths, etc. with an obvious
lexicographical order amongst the quarters, sixteenths, etc. Now, traverse
the list
 : for each portion of the square, choose the point
: for each portion of the square, choose the point
 such
that
such
that
 is in the portion, both
is in the portion, both
 and
and
 are in the list
are in the list
 , neither
has yet been used, and such that the latter occurring (in
, neither
has yet been used, and such that the latter occurring (in
 ) of them is
earliest possible, and amongst such the other one is the earliest possible.
) of them is
earliest possible, and amongst such the other one is the earliest possible.
To show that this works, it suffices to show that every point
 in the
square is in the boundary of
in the
square is in the boundary of
 . To show this, choose any open rectangle
containing
. To show this, choose any open rectangle
containing
 . If it is
. If it is
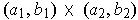 , let
, let
 . Let
. Let
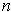 be chosen so
that
be chosen so
that
 . Then there is some
. Then there is some
 portion of the square
in
portion of the square
in
 which is entirely contained within the rectangle and containing
which is entirely contained within the rectangle and containing
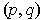 .
Since this part of the square contains an element of the set A and elements
not in A (anything in the portion with the same x-coordinate
.
Since this part of the square contains an element of the set A and elements
not in A (anything in the portion with the same x-coordinate
 works), it
follows that
works), it
follows that
 is in the boundary of
is in the boundary of
 .
.
 is the union of open intervals
is the union of open intervals
 such that each rational number in
such that each rational number in
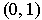 is contained in some
is contained in some
 ,
show that the boundary of
,
show that the boundary of
 is
is
 .
.
Clearly, the interior of
 is
is
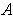 itself since it is a union of open sets;
also the exterior of
itself since it is a union of open sets;
also the exterior of
 clearly contains
clearly contains
 as
as
 .
Since the boundary is the complement of the union of the interior and the
exterior, it suffices to show that nothing in
.
Since the boundary is the complement of the union of the interior and the
exterior, it suffices to show that nothing in
 is in the exterior
of
is in the exterior
of
 . Suppose
. Suppose
 is in the exterior of
is in the exterior of
 . Let
. Let
 be an open interval containing
be an open interval containing
 and disjoint from
and disjoint from
 . Let
. Let
 be a rational
number in
be a rational
number in
 contained in
contained in
 . Then there is a
. Then there is a
 which contains
which contains
 , which is a contradiction.
, which is a contradiction.
 is a closed set that contains every rational number
is a closed set that contains every rational number
 ,
show that
,
show that
 .
.
Suppose
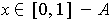 . Since
. Since
 is open, there is an open
interval
is open, there is an open
interval
 containing
containing
 and disjoint from
and disjoint from
 . Now
. Now
 contains a non-empty open subinterval of
contains a non-empty open subinterval of
 and this is necessarily
disjoint from
and this is necessarily
disjoint from
 . But every non-empty open subinterval of
. But every non-empty open subinterval of
 contains
rational numbers, and
contains
rational numbers, and
 contains all rational numbers in
contains all rational numbers in
 , which is
a contradiction.
, which is
a contradiction.
 is closed and bounded.
is closed and bounded.
Suppose
 is compact. Let
is compact. Let
 be the open cover consisting of
rectangles
be the open cover consisting of
rectangles
 for all positive integers
for all positive integers
 . Since
. Since
 is compact, there is a finite subcover
is compact, there is a finite subcover
 .
If
.
If
 , then
, then
 and so
and so
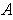 is bounded.
is bounded.
To show that
 is closed, it suffices its complement is open.
Suppose
is closed, it suffices its complement is open.
Suppose
 is not in
is not in
 .
Then the collection
.
Then the collection
 where
where
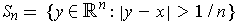 is an open cover of
is an open cover of
 . Let
. Let
 be a finite subcover. Let
be a finite subcover. Let
 .
Then
.
Then
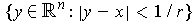 is an open neighborhood of
is an open neighborhood of
 which is disjoint from
which is disjoint from
 . So the complement of
. So the complement of
 is open, i.e.
is open, i.e.
 is closed.
is closed.
- If
 is closed and
is closed and
 , prove that there is a number
, prove that there is a number
 such
that
such
that
 for all
for all
 .
.
Such an
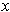 is in the exterior of
is in the exterior of
 , and so there is an open rectangle
, and so there is an open rectangle
 containing
containing
 and disjoint from
and disjoint from
 .
Let
.
Let
 .
This was chosen so that
.
This was chosen so that
 is
entirely contained within the open rectangle. Clearly, this means that
no
is
entirely contained within the open rectangle. Clearly, this means that
no
 can be
can be
 , which shows the assertion.
, which shows the assertion.
- If
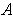 is closed,
is closed,
 is compact, and
is compact, and
 ,
prove that there is a
,
prove that there is a
 such that
such that
 for all
for all
 and
and
 .
.
For each
 , choose
, choose
 to be as in part (a). Then
to be as in part (a). Then
 is an open cover of
is an open cover of
 .
Let
.
Let
 be a finite subcover, and let
be a finite subcover, and let
 .
Then, by the triangle inequality, we know that
.
Then, by the triangle inequality, we know that
 satisfies the assertion.
satisfies the assertion.
- Give a counterexample in
 if
if
 and
and
 are required
both to be closed with neither compact.
are required
both to be closed with neither compact.
A counterexample:
 is the x-axis and
is the x-axis and
 is the graph of the
exponential function.
is the graph of the
exponential function.
 is open and
is open and
 is compact, show that there is
a compact set
is compact, show that there is
a compact set
 such that
such that
 is contained in the interior of
is contained in the interior of
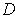 and
and
 .
.
Let
 be as in Problem 1-21 (b) applied with
be as in Problem 1-21 (b) applied with
 and
and
 .
Let
.
Let
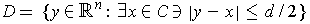 . It is
straightforward to verify that
. It is
straightforward to verify that
 is bounded and closed; so
is bounded and closed; so
 is compact.
Finally,
is compact.
Finally,
 is also true.
is also true.