 .
.
Let
 Then
Then
 is open and
Theorem 3-13 applies with
is open and
Theorem 3-13 applies with
 in place of the
in place of the
 in its statement.
Let
in its statement.
Let
 be a partition of unity subordinate to an admissible cover
be a partition of unity subordinate to an admissible cover
 of
of
 . Then
. Then
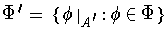 is a partion of unity subordinate to the cover
is a partion of unity subordinate to the cover
 . Now
. Now
 is absolutely convergent, and so
is absolutely convergent, and so
 also converges since the terms are identical. So,
also converges since the terms are identical. So,
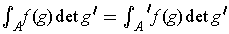 . By Theorem 3-14, we know that
. By Theorem 3-14, we know that
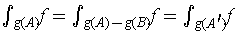 . Combining results, we get Theorem
3-13.
. Combining results, we get Theorem
3-13.
 and
and
 ,
prove that in some open set containing
,
prove that in some open set containing
 we can write
we can write
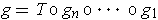 ,
where
,
where
 is of the form
is of the form
 , and
, and
 is a linear transformation. Show that we can write
is a linear transformation. Show that we can write
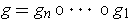 if and only if
if and only if
 is a diagonal matrix.
is a diagonal matrix.
We use the same idea as in the proof of Theorem 3-13. Let
 be a point
where
be a point
where
 . Let
. Let
 , and
, and
 .
Then
.
Then
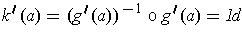 . Define for
. Define for
 ,
,
 . Then
. Then
 .
So we can define on successively smaller open neighborhoods of
.
So we can define on successively smaller open neighborhoods of
 , inverses
, inverses
 of
of
 and
and
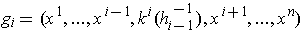 . One then can verify that
. One then can verify that
 .
Combining results gives
.
Combining results gives

and so
 .
.
Now, if
 is a diagonal matrix, then replace
is a diagonal matrix, then replace
 with
with
 .
for
.
for
 and
and
 . Then the
. Then the
 have the same form
as the
have the same form
as the
 and
and
 .
.
On the other hand, the converse is false. For example, consider the
function
 . Since
. Since
 is linear,
is linear,
 ; so
; so
 is not a diagonal matrix.
is not a diagonal matrix.
 by
by
 .
.
- Show that
 is 1-1, compute
is 1-1, compute
 , and show that
, and show that
 for all
for all
 . Show that
. Show that
 is the set
is the set
 of Problem 2-23.
of Problem 2-23.
Since
 , to show that the function
, to show that the function
 is 1-1,
it suffices to show that
is 1-1,
it suffices to show that
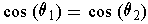 and
and
 imply
imply
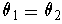 . Suppose
. Suppose
 .
Then
.
Then
 implies that
implies that
 (or
(or
 ). If
). If
 ,
it follows that
,
it follows that
 . But then
. But then
 and
and
 has the same value, contrary to hypothesis. So,
has the same value, contrary to hypothesis. So,
 is 1-1.
is 1-1.
One has

So,
 for all
for all
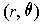 in the domain of
in the domain of
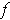 .
.
Suppose
 , i.e.
, i.e.
 and
and
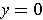 . If
. If
 ,
then
,
then
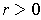 implies
implies
 and so
and so
 . But then
. But then
 contrary to hypothesis. On the other hand, if
contrary to hypothesis. On the other hand, if
 , then let
, then let
 and let
and let
 be the
angle between the positive
be the
angle between the positive
 -axis and the ray from (0,0) through
-axis and the ray from (0,0) through
 .
Then
.
Then
 .
.
- If
 , show that
, show that
 , where
, where


(Here
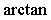 denotes the inverse of the function
denotes the inverse of the function
 .) Find P'(x,y). The function
.) Find P'(x,y). The function
 is called the polar
coordinate system on
is called the polar
coordinate system on
 .
.
The formulas for
 and
and
 follow from the last paragraph
of the solution of part (a). One has
follow from the last paragraph
of the solution of part (a). One has
 . This is trivial
from the formulas except in case
. This is trivial
from the formulas except in case
 . Clearly,
. Clearly,
 .
Further,
L'H@ocirc;pital's Rule allows one to calculate
.
Further,
L'H@ocirc;pital's Rule allows one to calculate
 when
when
 by
checking separately for the limit from the left and the limit from the right.
For example,
by
checking separately for the limit from the left and the limit from the right.
For example,
 .
.
- Let
 be the region between the circles of radii
be the region between the circles of radii
 and
and
 and the half-lines through 0 which make angles of
and the half-lines through 0 which make angles of
 and
and
 with the
with the
 -axis. If
-axis. If
 is integrable and
is integrable and
 , show that
, show that
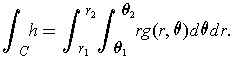
If
 , show that
, show that

Assume that
 and
and
 .
Apply Theorem 3-13 to the map
.
Apply Theorem 3-13 to the map
 by
by
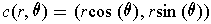 . One has
. One has
 and
and
 . So the first identity holds. The second identity
is a special case of the first.
. So the first identity holds. The second identity
is a special case of the first.
- If
 , show that
, show that

and

For the first assertion, apply part (c) with
 .
Then
.
Then
 . Applying (c) gives
. Applying (c) gives
 .
.
The second assertion follows from Fubini's Theorem.
- Prove that

and conclude that

One has
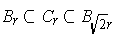 and the integrands are
everywhere positive. So
and the integrands are
everywhere positive. So

Since part (d) implies that
 , the squeeze principle
implies that
, the squeeze principle
implies that
 also.
also.
But using part (d) again, we get
 also exists and is
also exists and is
 (since the square root function is
continuous).
(since the square root function is
continuous).