Exercises: Chapter 3, Section 5

    1. Suppose that ch3e1.png is a non-negative continuous function. Show that ch3e2.png exists if and only if ch3e3.png exists.

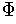      For ch3e4.png a natural number, define ch3e5.png and ch3e6.png . Consider a partition of unity ch3e7.png subordinate to the cover ch3e8.png . By summing the ch3e9.png with the same ch3e10.png in condition (4) of Theorem 3-11, one can assume that there is only one function for each ch3e11.png , let it be ch3e12.png . Now ch3e13.png exists if and only ch3e14.png converges. But ch3e15.png . So the sum converges if and only if ch3e16.png exists.

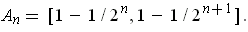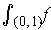    2. Let ch3e17.png Suppose that ch3e18.png satisfies ch3e19.png and ch3e20.png for all ch3e21.png . Show that ch3e22.png does not exist, but ch3e23.png .

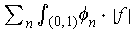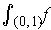      Take a partition of unity ch3e24.png subordinate to the cover ch3e25.png where ch3e26.png for ch3e27.png . As in part (a), we can assume there is only one ch3e28.png as in condition (4) of Theorem 3-11. Consider the convergence of ch3e29.png . One has ch3e30.png where ch3e31.png . It follows that the sum in the middle does not converge as ch3e32.png and so ch3e33.png does not exist.

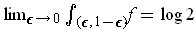      The assertion that ch3e34.png . If not necessrily true. From the hypothesis, we only know the values of the integral of ch3e35.png on the sets ch3e36.png , but don't know how ch3e37.png behaves on other intervals -- so it could be that ch3e38.png may not even exist for all ch3e39.png To correct the situation, let us assume that ch3e40.png is of constant sign and bounded on each set ch3e41.png . Then ch3e42.png is bounded on each interval ch3e43.png and so by Theorem 3-12, the integral in the extended sense is same as the that in the old sense. Clearly, the integral in the old sense is monotone on each interval of ch3e44.png , and the limit is just ch3e45.png .

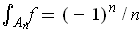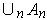  2. Let ch3e46.png be a closed set contained in ch3e47.png . Suppose that ch3e48.png satisfies ch3e49.png and ch3e50.png outside ch3e51.png . Find two partitions of unity ch3e52.png and ch3e53.png such that ch3e54.png and ch3e55.png converge absolutely to different values.

    The sums ch3e56.png and ch3e57.png have terms of the same sign and are each divergent. So, by re-ordering the terms of ch3e58.png , one can make the sum approach any number we want; further this can be done so that there are sequences of partial sums which converge monotonically to the limit value. 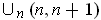By forming open covers each set of which consists of intervals ch3e59.png for the sum of terms added to each of these partial sums, one gets covers of ch3e60.png . Because ch3e61.png is zero outside ch3e62.png , one can `fatten' up the covering sets so that they are a cover of the real numbers no smaller than 1 without adding any points where ch3e63.png is non-zero. Finally, one can take a partition of unity subordinate to this cover. By using arrangements with different limiting values, one gets the result.