 be a set of content 0. Let
be a set of content 0. Let
 be the set of all
be the set of all
 such that
such that
 is not of content 0. Show that
is not of content 0. Show that
 is a set of measure 0.
is a set of measure 0.
Following the hint,
 is integrable with
is integrable with
 by Problem 3-15 and Fubini's Theorem.
We have
by Problem 3-15 and Fubini's Theorem.
We have
 . Now
. Now
 is equivalent to
the condition that either
is equivalent to
the condition that either
 or
or
 .
Both of these having integral 0 implies by Problem 3-18 that the sets where
their integrand is non-zero are of measure 0, and so
.
Both of these having integral 0 implies by Problem 3-18 that the sets where
their integrand is non-zero are of measure 0, and so
 is also of measure 0.
is also of measure 0.
 be the union of all
be the union of all
 where
where
 is a rational number in
is a rational number in
 written in lowest terms. Use
written in lowest terms. Use
 to show that the word ``measure" in Problem 3-23 cannot be replaced with ``content".
to show that the word ``measure" in Problem 3-23 cannot be replaced with ``content".
The set
 is the set of rational numbers in
is the set of rational numbers in
 which is of measure 0,
but not of content 0, because the integral of its characteristic function does
not exist. To see that the set
which is of measure 0,
but not of content 0, because the integral of its characteristic function does
not exist. To see that the set
 has content 0, let
has content 0, let
 . Let
. Let
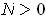 be such that
be such that
 . Then the set
. Then the set
 can be covered by
the rectangles
can be covered by
the rectangles
 and for each
and for each
 in lowest terms
with
in lowest terms
with
 , the rectangle
, the rectangle
 where
where
 . The sum of the areas of these rectangles
is less than
. The sum of the areas of these rectangles
is less than
 .
.
 that
that
 is not a set of measure 0 (or content 0) if
is not a set of measure 0 (or content 0) if
 for each
for each
 .
.
This follows from Problem 3-8 and Theorem 3-6, but that is not an induction.
Fubini's Theorem and induction on
 show that
show that
 and so
and so
 does not have content 0, and hence is not of measure 0.
does not have content 0, and hence is not of measure 0.
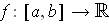 be integrable and non-negative,
and let
be integrable and non-negative,
and let
 . Show
that
. Show
that
 is Jordan measurable and has area
is Jordan measurable and has area
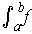 .
.
One has
 and so by Fubini,
and so by Fubini,
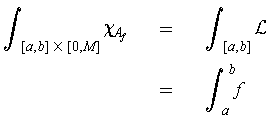
where
 is an upper bound on the image of
is an upper bound on the image of
 .
.
 is continuous, show that
is continuous, show that

where the upper bounds need to be determined.
By Fubini, the left hand iterated integral is just
 where
where

Applying Fubini again,
shows that this integral is equal to
 .
.
 if these are continuous.
if these are continuous.
Following the hint, if
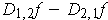 is not zero for some
point
is not zero for some
point
 , then we may assume (by replacing
, then we may assume (by replacing
 with
with
 if necessary that
it is positive at
if necessary that
it is positive at
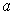 . But then continuity implies that it is positive on
a rectangle
. But then continuity implies that it is positive on
a rectangle
 containing
containing
 . But then its integral over
. But then its integral over
 is also positive.
is also positive.
On the other hand, using Fubini on
 gives:
gives:

Similarly, one has
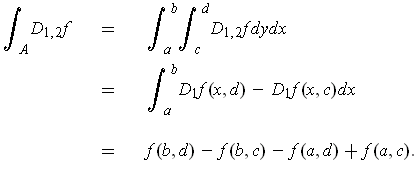
Subtracting gives:
 which is a contradiction.
which is a contradiction.
 obtained by revolving a Jordan measurable set in the
obtained by revolving a Jordan measurable set in the
 -plane about the
-plane about the
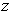 -axis.
-axis.
To avoid overlap, it is convenient to keep the set in the positive
 half
plane. To do this, let
half
plane. To do this, let
 be the original Jordan measurable set in the
be the original Jordan measurable set in the
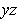 -plane, and replace it with
-plane, and replace it with
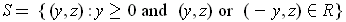 .
Theorem 3-9 can be used to show that
.
Theorem 3-9 can be used to show that
 is Jordan measurable if
is Jordan measurable if
 is.
is.
The problem appears to be premature since we really want to be able to
do a change of variables to cylindrical coordinates. Assuming that we
know how to do that, the result becomes
 .
.
 be the set in Problem 1-17. Show that
be the set in Problem 1-17. Show that

but that
 does not exist.
does not exist.
The problem has a typo in it; the author should not have switched the order
of the arguments of
 as that trivializes the assertion.
as that trivializes the assertion.
The iterated integrals are zero because the inside integral is the zero function. The last integral cannot exist by Theorem 3-9 and Problem 1-17.
 and
and
 is continuous, define
is continuous, define
 by
by

What is
 , for
, for
 in the interior of
in the interior of
 ?
?
Let
 be in the interior of
be in the interior of
 , fix
, fix
 . We have
. We have
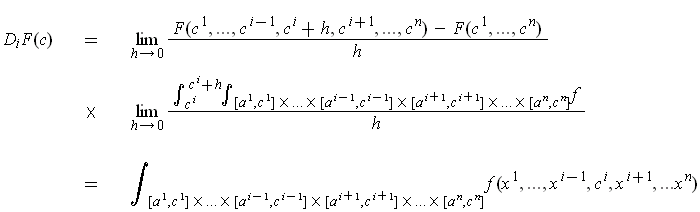
by Fubini's Theorem.
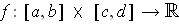 be continuous and
suppose
be continuous and
suppose
 is continuous. Define
is continuous. Define
 . Prove
Leibnitz' Rule:
. Prove
Leibnitz' Rule:
 .
.
Using the hint, we have
 .
One has
.
One has

 is continuous and
is continuous and
 is continuous, define
is continuous, define
 .
.
- Find
 and
and
 .
.
One has
 and
and
 where the second
assertion used Problem 3-32.
where the second
assertion used Problem 3-32.
- If
 , find
, find
 .
.
We have
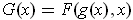 and so by the chain rule one has
and so by the chain rule one has

 be continuously
differentiable and suppose
be continuously
differentiable and suppose
 . As in Problem 2-21, let
. As in Problem 2-21, let

Show that
 .
.
One has

- Let
 be a linear transformation
of one of the following types:
be a linear transformation
of one of the following types:



If
 is a rectangle, show that the volume of
is a rectangle, show that the volume of
 is
is
 .
.
In the three cases,
 is
is
 , 1, and 1 respectively. If the original
rectangle
, 1, and 1 respectively. If the original
rectangle
 , then
, then
 is
is

in the first case, is a cylinder with a parallelogram base in the second case, and is the same rectangle except that the intervals in the
 and
and
 places are swapped in the third case. In the second case, the parallelogram
base is in the
places are swapped in the third case. In the second case, the parallelogram
base is in the
 and
and
 directions and has corners
directions and has corners
 . So the volumes
do not change in the second and third case and get multiplied by
. So the volumes
do not change in the second and third case and get multiplied by
 in the
first case. This shows the result.
in the
first case. This shows the result.
- Prove that
 is the volume of
is the volume of
 for any linear
transformation
for any linear
transformation
 .
.
If
 is non-singular, then it is a composition of linear transformations
of the types in part (a) of the problem. Since
is non-singular, then it is a composition of linear transformations
of the types in part (a) of the problem. Since
 is multiplicative,
the result follows in this case.
is multiplicative,
the result follows in this case.
If
 is singular, then
is singular, then
 is a proper subspace of
is a proper subspace of
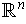 and
and
 is a compact set in this proper subspace. In particular,
is a compact set in this proper subspace. In particular,
 is contained in a hyperplane. By choosing the coordinate properly, the
hyperplane is the image of a linear transformation from
is contained in a hyperplane. By choosing the coordinate properly, the
hyperplane is the image of a linear transformation from
 into
into
 made up of a composition of maps of the first two types.
This shows that the compact portion of the hyperplane is of volume 0. Since
the determinant is also 0, this shows the result in this case too.
made up of a composition of maps of the first two types.
This shows that the compact portion of the hyperplane is of volume 0. Since
the determinant is also 0, this shows the result in this case too.
 and
and
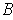 be Jordan measurable
subsets of
be Jordan measurable
subsets of
 . Let
. Let
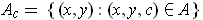 and define
and define
 similarly. Suppose that each
similarly. Suppose that each
 and
and
 are Jordan measurable
and have the same area. Show that
are Jordan measurable
and have the same area. Show that
 and
and
 have the same volume.
have the same volume.
This is an immediate consequence of Fubini's Theorem since the inside integrals are equal.